Quickly Master Complex Engineering Concepts
Whether you’re just starting out on your engineering journey or are an experienced professional, our aim is to provide you with all the resources you need to master tricky engineering concepts.

Step 1 – Learn
Learn the fundamentals of mechanical and civil engineering with the help of our articles and videos


Step 2 – Test
Check your understanding of different engineering topics using our detailed quizzes


Step 3 – Improve
Use resources like our summary sheets to continually develop and improve your knowledge

Not sure where to start? Here are a few featured topics that cover a range of interesting engineering concepts.
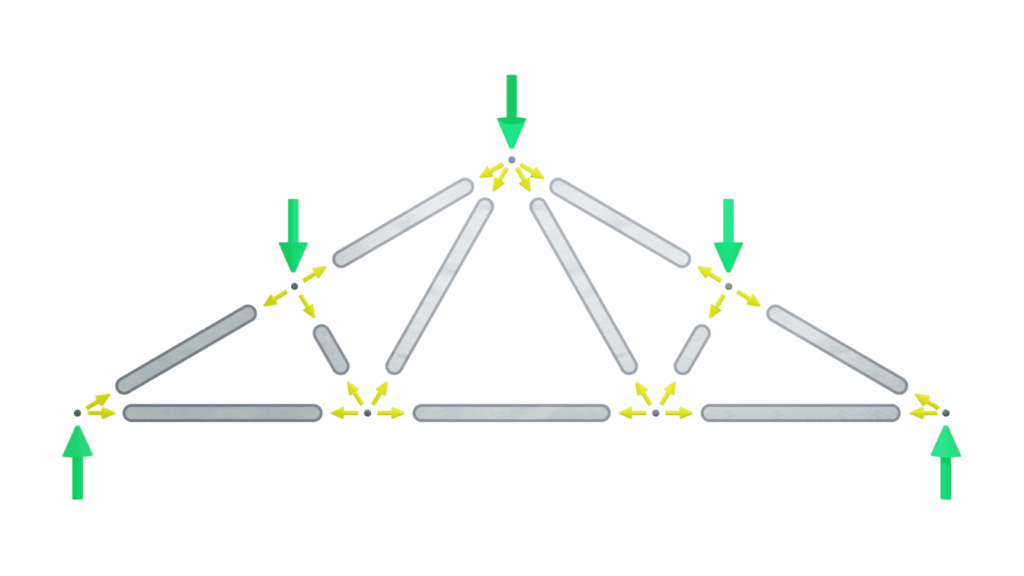
Trusses
Trusses are structures (e.g bridges or roofs) made up of members that can only carry tensile or compressive axial loads.
Buckling
Buckling is a sudden deflection that occurs in slender columns or members that are loaded in compression.
The Finite Element Method
The finite element method is a numerical method used to approximate the solution to complex problems governed by differential equations.
Thermal Radiation
Radiation is the heat transfer mode where an object emits energy in the form of electromagnetic radiation due to its temperature.
The Efficient Engineer summary sheets are designed to present all of the key information you need to know about a particular engineering topic on a single page. It doesn’t get more efficient than that!
You can use them as study aids, or just as handy references guides for whenever you need to brush up on a troublesome topic.


Watch the latest video from the Efficient Engineer YouTube channel.
The Incredible Properties of Composite Materials
The latest Efficient Engineer video covers composite materials.
This video explores the different types of composites, and how their use to create materials with incredible properties has completely transformed how some of the most advanced enginering problems can be solved.
Test your understanding of engineering concepts with the question of the day.
Testing was performed in a laboratory to determine the fatigue performance of steel, copper, aluminium and brass samples. The test results were used to generate S-N curves for each material, but the curves were not labelled correctly. Which material does the S-N curve below correspond to?
Steel
Aluminium
Brass
Copper
The fatigue performance of steel and other ferrous alloys is such that when it is cycled below a certain level, the number of cycles to failure is theoretically infinite. The stress level below which this occurs is called the endurance limit.
Aluminium, brass and copper do not have an endurance limit. Even for very small stress ranges the material will eventually fail due to fatigue.
As the S-N curve exhibits a clear endurance limit, it must correspond to the testing performed for steel.




