Understanding Buckling

Buckling is an important topic that any engineer designing structures that carry compressive loads must understand.

This page will guide you through the basics of buckling, from Euler’s formula for predicting the onset of buckling to more complex topics like slenderness ratios and inelastic buckling. So keep reading, or watch the animated video below, to get up to speed.

Understanding Buckling (https://www.youtube.com/watch?v=21G7LA2DcGQ)

What is Buckling?

Buckling is the sudden deformation of a structural member that is loaded in compression, that occurs when the compressive load in the member reaches a critical value.

Buckling often occurs suddenly, and can produce large displacements. This doesn’t always result in yielding or fracture of the material, but buckling is still considered to be a failure mode since the buckled structure can no longer support a load in the way it was originally intended to.

A structural member that has buckled due to a compressive load

Any long structural member that is loaded in compression is at risk of failing due to buckling. Columns are common examples of structures that may fail by buckling. Individual members in trusses are frequently loaded in compression, so trusses are another example of a structure at risk of failure due to buckling.

Columns and members of a truss that are loaded in compression are examples of structures that are at risk of failing due to buckling

Euler’s Buckling Formula

Euler’s buckling formula is a simple equation that is used to calculate the axial load $P_{c r}$ at which a column or beam will buckle. At the critical buckling load any small perturbation, whether it’s a lateral force or a small imperfection in the column geometry, will cause the column to buckle.

Euler’s Buckling Formula

P_{c r} = \frac{π^{2} E I}{{L_{e}}^{2}}

The critical load depends on only three parameters, the Young’s modulus $E$ of the column material, the second moment of area $I$ of the column cross-section, and the effective length $L_{e}$ of the column.

You can use our critical buckling force calculator to see how the different input parameters affect how much force a column can carry.

The figure below illustrates how a column with a critical buckling load of 1000 kN will buckle.

Column with a critical buckling load $P_{c r}$ of 1000 kN

Test Your Understanding

A column is being designed to support a platform, but elastic buckling is a concern. Which of the following proposed options can be used to reduce the risk of buckling?

Choose a material with a lower Young's modulus

Increase the length of the column

Modify the cross-section to increase the second moment of area

Choose a material with a higher yield strength

Explanation

The Euler critical buckling force is calculated using the following equation:

$P_{} = \frac{π^{2} E I}{{L_{e}}^{2}}$

Of the proposed options only modifying the cross-section to increase the second moment of area will increase the critical buckling, and so will reduce the risk of buckling.

Reducing Young’s modulus or increasing the column length will reduce the critical buckling force. And since we are dealing with elastic buckling the yield strength of the material is irrelevant.

Effective Length and End Conditions

The way the ends of a column or beam are restrained will affect the critical buckling load. A column that is fixed at one end and free at the other will clearly only be able to support a much smaller load before buckling compared to one that is pinned at both ends. The buckled shapes are also quite different.

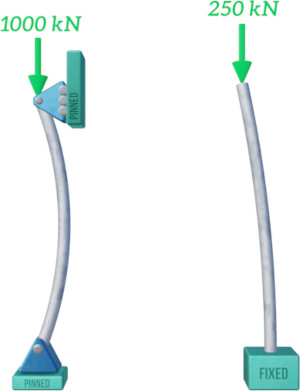
Critical buckling loads for a column pinned at both ends and for a column fixed at one end

Euler’s formula accounts for different end conditions using the effective length parameter $L_{e}$ .

A column that is pinned at both ends has an effective length that is equal to the length of the column $L$ . Other end conditions result in an effective length that is equal to the length $L$ multiplied by a specific factor. These factors are shown in the table below for a few different end conditions.

End Condition
Effective Length	$L_{e} = 0.5 L$	$L_{e} = L$	$L_{e} = 2 L$	$L_{e} = 0.7 L$

The Efficient Engineer Summary Sheets

The Efficient Engineer summary sheets are designed to present all of the key information you need to know about a particular topic on a single page. It doesn’t get more efficient than that!

Get The Summary Sheets!

Slenderness Ratio

Even without knowing anything about Euler’s formula it’s intuitively quite obvious that slender columns are at much greater risk of buckling than stocky ones. This is why members of a truss that are in compression are sometimes designed to be thicker than those in tension, and why bracing members are used to prevent buckling of long compressive members.

Euler’s formula confirms this intuition – the length term in the equation is squared, and as a result doubling the length of a column means that it can only support a quarter of the load before buckling.

Difference in critical buckling load where one column is half the length of the other

To better understand the effect of slenderness it’s useful to introduce a non-dimensional parameter called the slenderness ratio, that defines how slender the column is (i.e. how thin it is compared to its length).

Effective Slenderness Ratio

\frac{L_{e}}{r}

The $r$ term is the radius of gyration of the column and is defined as the square root of the second moment of area $I$ divided by the cross-sectional area $A$ .

$r = \sqrt{\frac{I}{A}}$

If we divide the Euler critical buckling force by the column cross-sectional area we obtain the Euler critical buckling stress $σ_{c r}$ , which is the normal stress in the column at which buckling will occur.

$σ_{c r} = \frac{P_{c r}}{A}$

$σ_{c r} = \frac{π^{2} E I}{A {L_{e}}^{2}}$

By introducing the slenderness ratio we obtain this form of the equation for $σ_{c r}$ :

$σ_{c r} = \frac{π^{2} E}{(L_{e} / r)^{2}}$

As mentioned earlier it’s intuitive that the slenderness of a column will significantly affect how much load it can support before buckling, so it’s interesting to take a look at how the Euler critical buckling stress varies with the slenderness ratio – this is shown in the graph below.

Critical buckling stress vs slenderness ratio

Very slender columns have a large slenderness ratio and a very low critical buckling stress. For stocky columns with low slenderness ratios the critical buckling stress will be very large.

The dashed horizontal line on the graph above shows the compressive yield strength of the column material, $σ_{y}$ . For very low slenderness ratios the strength of the material will be exceeded before the buckling limit is reached. This means we can define two distinct regions, one where columns fail by crushing because the stress in the column exceeds the material yield strength (i.e. for stocky columns), and one where they fail due to buckling (i.e. for slender columns).

This curve only represents the theoretical behaviour of columns. If we plot buckling stresses determined experimentally for real columns we can see it doesn’t exactly match the theoretical behaviour – this is shown in the graph below. In particular the transition between plastic failure (crushing) and elastic failure (buckling) is much more gradual. This is because for columns in this transition range, buckling is actually a complex combination of these two failure modes. Buckling in this transition region is called inelastic buckling, and it should be modelled using methods like Engesser’s theory or Shanley’s theory, rather than Euler’s formula.

The gap between the experimental results and the theoretical results is large in the inelastic buckling region, where failure is a complex combination of the plastic failure (crushing) and elastic failure (buckling) modes

Many industry design codes include curves similar to the ones shown above that can be used for the design of members loaded in compression.

What is Buckling?

Euler’s Buckling Formula

Effective Length and End Conditions

Slenderness Ratio

Related Topics

Download your FREE Strength of Materials Equation Sheet