Understanding Young’s Modulus

Material PropertiesLast updated: March 12, 2024

Quick Summary

Young’s modulus is an important material property in engineering:

It is a measure of the stiffness of a material (i.e. a measure of how much a material will deform when acted on by a force).
Metals and ceramic materials tend to have high Young’s modulus values, whereas polymers have much lower values (they deform more for the same applied load)
In the elastic region of the stress-strain curve the slope of the curve is equal to Young’s modulus. Young’s modulus can be calculated as an applied stress divided by the resulting strain – this equation is called Hooke’s Law.

Young’s modulus is a really important material property that appears all the time in engineering and physics. It’s used for everything from calculating when a column will buckle to determining how much a beam will deflect when forces are applied to it. So let’s learn more about it!

What is Young’s Modulus?

Young’s modulus, also called the elastic modulus, is a material property that describes how much a material will deform when a load is applied to it. It is essentially a measure of how stiff a material is.

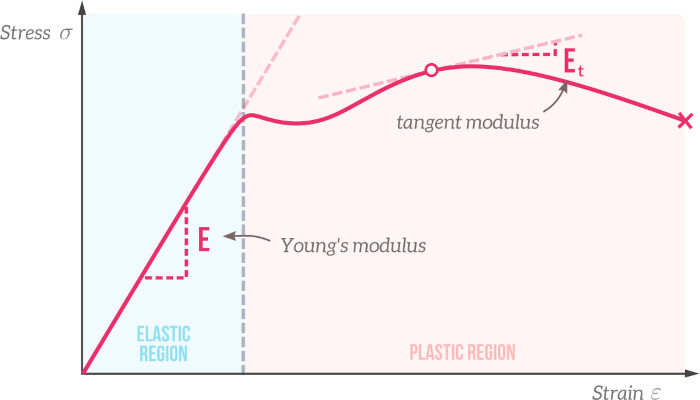
The easiest way to visualise Young’s modulus is on a stress-strain curve, shown in the image below, that can be obtained by performing a tensile test on a sample. The curve can be divided into two regions, an elastic region and a plastic region. If the applied stress is low and we remain in the elastic region – the original dimensions of the material will be completely recovered when the applied load is removed. For larger stresses that take us into the plastic region, permanent plastic deformation will remain after the applied load is removed.

The stress-strain curve is a straight line in the elastic region for most materials. The slope of this curve is equal to Young’s modulus, which is denoted using the letter $E$. Young’s modulus describes the relationship between stress and strain in the elastic region. The higher the Young’s modulus of a material, the smaller the elastic deformations (strain) will be for a given applied load (stress).

Stress-strain curve for mild steel showing how Young's modulus is equal to the slope of the curve in the elastic region. The elastic and plastic regions are shown in different colors. — A material’s Young’s modulus is equal to the slope of its stress-strain curve in the elastic region

Hooke’s law gives us the relationship between stress and strain in the linear elastic region of the stress-strain curve.

Hooke’s Law

$$\sigma = E \varepsilon$$

Since strain is dimensionless, Young’s modulus has the same units as stress. Steel has a high Young’s modulus of around 200 GPa, whereas Polystyrene has a low Young’s modulus of around 3 GPa.

Check out the video below if you want to watch an animated summary of all of this information about Young’s modulus. If not, just keep reading!

https://www.youtube.com/watch?v=DLE-ieOVFjI

Understanding Young's Modulus (https://www.youtube.com/watch?v=DLE-ieOVFjI)

Applications of Young’s Modulus

Young’s modulus is very important when it comes to engineering, because so often engineering design and analysis involves determining how much something will deform. A high Young’s modulus value is good if you want deformations to be very small – you wouldn’t want a bridge to deform much when a car passes over it, for example, so it would make sense to construct the bridge from materials with a high Young’s modulus.

Because it defines the relationship between stress and strain, Young’s modulus appears in all kinds of different equations that are commonly used in mechancal and civil engineering. Here are a few examples:

Buckling Formula

This equation describes the critical load at which a column will buckle

$$P_{cr} = \frac{\pi^2 EI}{{L_e}^2}$$

Beam Deflection

This equation describes how much a beam will deflect due to applied loads

$$\frac{d^2y}{dx^2} = \frac{M}{EI}$$

Axial Deformation

This equation describes how much a bar will deform when an axial load is applied to it

$$\delta = \frac{FL}{AE}$$

How to Determine Young’s Modulus

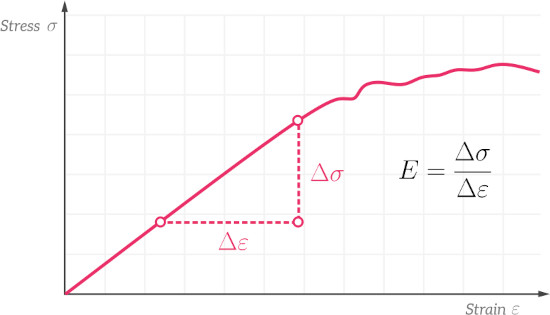
If you have data from tensile tests performed for a particular material, it’s easy to figure out what the Young’s modulus for that material is. All you have to do is take two points in the linear elastic part of the stress-strain curve, and use those points to measure the slope of the curve. This is illustrated in the figure below.

Stress-strain curve illustrating how Young's modulus can be determined from experimental data. — How to calculate Young’s modulus from test data

Young’s Modulus Values for Different Materials

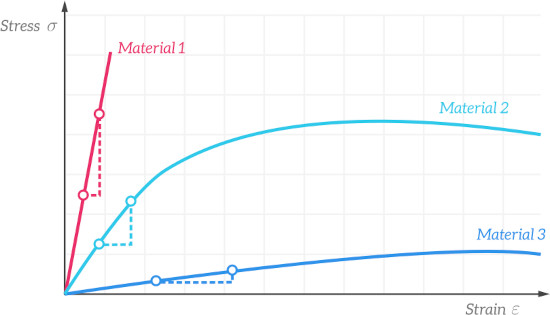
The image below shows stress-strain curves for a few different materials. Material 1 has the steepest slope in the elastic region, which means that it has the largest Young’s modulus – you will need to apply a much larger force to deform Material 1 than you would to deform Materials 2 or 3 by the same amount. The stress-strain curve for Material 1 is typical of diamond, for example, whereas Material 2 is more like steel, and Material 3 is typical of a material like rubber.

Stress-strain curves for three different materials, with very different Young's modulus values — Material 1 has the largest Young’s modulus (it has the highest stiffness)

The table below shows typical Young’s modulus values for a few different materials. Ceramics and metals generally tend to have quite high Young’s modulus values, meaning that they are quite stiff. Polymers on the other hand have much lower values.

Material	Young’s Modulus [GPa]
Rubber	0.1
Polystyrene	3
Aluminium Alloy	69
Titanium	120
Copper	130
Carbon Steel	207
Tungsten Carbide	600
Diamond	1200

Understanding Young’s Modulus Using the Ball-and-Spring Model

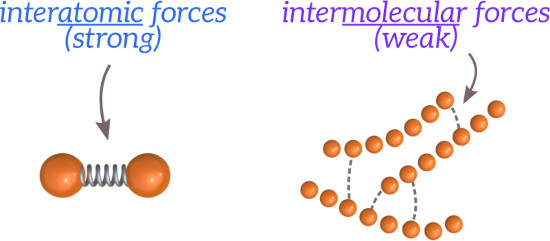
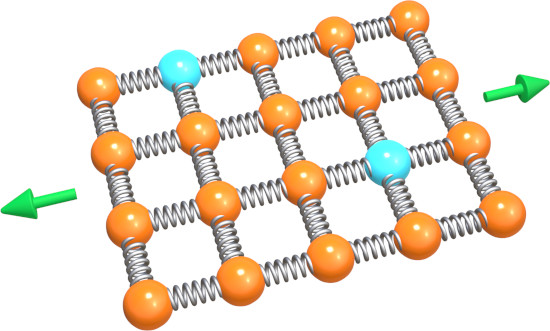
The Young’s modulus of a material is closely related to the strength of the bonds between its atoms. We can think of these interatomic bonds as small springs connecting adjacent atoms, represented by balls.

Grid of spheres which are connected together using springs. — In the ball-and-spring model the atoms are represented by balls and the interatomic forces are represented by springs.

When a force is applied to the material, deformation of the material is resisted by the stiffness of the interatomic bonds. Young’s modulus is a measure of how strong the interatomic bonds are, or in other words it is a measure of how stiff the springs between the atoms are. When the force is removed the atoms return to their initial position – this is elastic deformation.

The mechanism behind plastic deformation is very different, because it involves the breaking of bonds and the re-arrangement of the position of the atoms.

Elastic Deformation

caused by the stretching of the bonds between atoms
deformation is reversed when the load is removed

Plastic Deformation

caused by interatomic bonds breaking at dislocations
deformation is permanent and remains after the load is removed.

As well as helping us understanding the differences between elastic and plastic deformation, the ball-and-spring model can help us answer a few important questions about Young’s modulus.

Why is Young’s Modulus Different for Different Materials?

The strength of the bonds between the consituent atoms or molecules of a material (i.e. the stiffness of the springs in the ball-and-spring model) plays a big role in determining the Young’s modulus of a material.

The strength of these bonds is affected by atomic/molecular structure and chemical composition, which is why Young’s modulus values can be so different for different materials.

The way the atoms and molecules are bonded also plays a big role. Polymers for example have lower Young’s modulus values compared to metals and ceramics because the material stiffness is determined by the much the weaker intermolecular bonds, instead of the strong interatomic bonds.

On the left two spheres connecting by a stiff spring are used to illustrate the strong interatomic forces. On the right weak intermolecular forces are shown between spheres. — Polymers have low Young’s modulus values because the stiffness of the material is governed by weak intermolecular forces instead of strong interatomic forces

Does Young’s Modulus Change for Different Metal Alloys?

The ball-and-spring model also explains why Young’s modulus values tend to be very similar for different alloys of the same metals. Carbon steel for example has many different alloys that have very different yield and tensile strengths, but they all have very similar Young’s modulus values. This is because these alloys usually contain only very small concentrations of the alloying elements, that have little effect on the overall stiffness of the atomic bonds. Carbon steel is an interstitial alloy, but the same is true for substitional alloys, like the one shown below.

Grid of spheres which are connected together using springs, but some of the spheres are colored differently to indicate that this is a substitutional alloy. — This substitional alloy contains only very small concentrations of the blue alloying elements, so the alloying elements don’t significantly affect the overall stiffness of the material

Test Your Understanding

Which of the following significantly affect the Young's modulus of steel?

None of these

Alloying

Heat treatment

Work hardening

Explanation

The Young's modulus of a material is related to the strength of its atomic bonds. This is not significantly affected by alloying in steels due to the small proportion of alloying elements, and it is also not affected by heat treatment or work hardening. This is why all steels have a Young's modulus of around 207 GPa.

How Does Young’s Modulus Vary with Temperature?

For most materials, Young’s modulus decreases as temperature increases. This is because an increase in temperature causes an increase in the vibrations of atoms, which increases the spacing between them, reducing the strength of the interatomic bonds.

Carbon steel for example has a Young’s modulus of 200 GPa at room temperature, but this reduces to around 150 GPa at 600°C.

Young’s Modulus vs Tangent Modulus

The tangent modulus is a material property that is closely related to Young’s modulus. Whereas Young’s modulus is the slope of the stress-strain curve in the elastic region, the tangent modulus is defined as the slope of the stress-strain curve at any point along the curve, whether that’s in the elastic or the plastic region. The value of the tangent modulus changes as you move along the stress-strain curve.

In the linear elastic region of the stress-strain curve the tangent modulus is equal to Young’s modulus. Outside of this region the tangent modulus is smaller than Young’s modulus, because materials tend to soften and become less stiff as they deform plastically.

A stress-train curve for mild steel showing the different between Young's modulus in the elastic region and the tangent modulus in the plastic region. — The tangent modulus is defined as the slope of the stress-strain curve. Unlike Young’s modulus, which is a constant value, the tangent modulus varies along the stress-strain curve.

The tangent modulus can be calculated from stress-strain curves obtained from testing, or can be calculated analytically using methods like the Ramberg-Osgood equation.