Area Moment of Inertia Calculator

This calculator is used to calculate the area moment of inertia, or second moment of area, for a range of different beam cross-sections and bending axes. The area moment of inertia is a parameter that defines how much resistance the cross-section of a beam has to bending because of its geometry.

Circular Cross-Section | Bending axes pass through centroid

$I_{xx} = I_{yy} = \frac{\pi r^4}{4}$

Radius r:

Input units:

Second moment of area I_xx: Second moment of area I_yy:

Output units:

Hollow Circular Cross-Section | Bending axes pass through centroid

$I_{xx} = I_{yy} = \frac{\pi}{4} ({r}^4 - (r - t)^4)$

Radius r: Thickness t:

Input units:

Second moment of area I_xx: Second moment of area I_yy:

Output units:

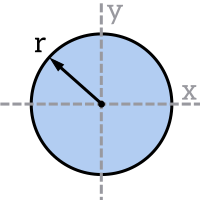
Rectangular Cross-Section | Bending axes pass through centroid

$I_{xx} = \frac{bh^3}{12}$ $I_{yy} = \frac{b^3h}{12}$

Height h: Width b:

Input units:

Second moment of area I_xx: Second moment of area I_yy:

Output units:

I-Beam Cross-Section | Bending axes pass through centroid

$I_{xx} = \frac{b(d+2t)^3}{12}-\frac{(b-t_w)d^3}{12}$ $I_{yy} = \frac{b^3t}{6}+\frac{{t_w}^3d}{12}$

Width b: Inner Height d: Flange Thickness t: Web Thickness t_w:

Input units:

Second moment of area I_xx: Second moment of area I_yy:

Output units:

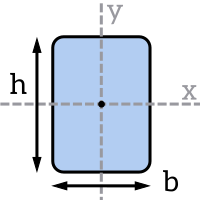
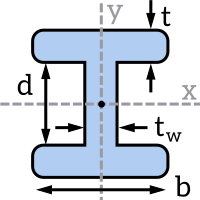
Remember that the parallel axis theorem can be used to calculate $I$ for different bending axes. It states that the area moment of inertia about any axis $I_x$ can be calculated from the area moment of inertia about a parallel axis $I_{xc}$ that passes through the centroid of the cross-section, the area of the cross-section $A$ and the distance between the two axes $d$. Have a read of our page on the area moment of inertia to learn more about how the parallel axis theorem works.

Parallel Axis Theorem

$$I_x = I_{xc} + Ad^2$$

Related Topics

Download your FREE Strength of Materials Equation Sheet