Stress and strain are fundamental concepts in engineering, and in strength of materials in particular, that describe how an object responds to applied loads. This page covers the basics, which are also summarised in the following video:
What is Stress?
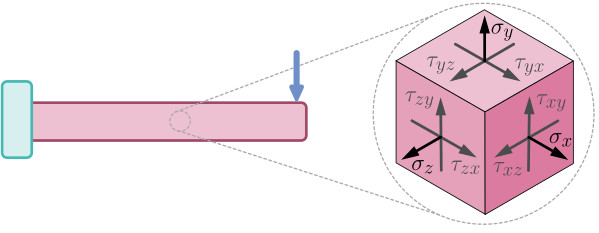
When a body like the bar shown below is loaded by external forces, internal forces develop within it to resist the applied forces. We can visualise these forces by making an imaginary cut through the object. The internal forces develop in such a way that they balance the external forces, to maintain equilibrium.


Instead of discussing the magnitude of these imaginary internal forces, it’s more useful to talk about how the internal forces are distributed over a surface, using a parameter called stress, that quantifies the internal force per unit area. Stress describes the distribution of internal forces within a body.
The concept of stress gives us a way of describing the internal state that develops within a body as it responds to externally applied loads. This is important because it allows us to predict when an object will fail. By comparing the stress in a body with the yield or ultimate strengths of the material, obtained from tests, we can estimate how close an object is to deforming permanently or to fracturing. Using stress to predict failure is covered in more detail in the page on failure theories.
Stress is split into two different types, normal stress and shear stress, that depends on whether the internal forces are perpendicular or parallel to the surface of interest.
Normal Stress
The type of stress where the internal forces act perpendicular to a surface, like for the bar shown above, is called normal stress. This type of stress is denoted using the symbol $\sigma$ (the greek letter sigma), and is calculated as the force divided by the area over which it acts.
Stress is a measure of the internal force per unit area, so it has units of Newtons per square meter ($\mathrm{N/m^2}$) in SI units and pounds per square inch in US units. Units of $N/m^2$ are also called Pascals ($\mathrm{Pa}$).
Normal stresses can be either tensile, when the object is getting stretched, or compressive, when it is getting compressed.
Shear Stress
The type of stress where the internal forces act parallel to a surface is called shear stress.


It can be calculated in a similar way to normal stress, as the applied force $F$ divided by the cross-sectional area $A$. Shear stress is denoted using the symbol $\tau$ (the greek letter tau).
The Efficient Engineer Summary Sheets
The Efficient Engineer summary sheets are designed to present all of the key information you need to know about a particular topic on a single page. It doesn’t get more efficient than that!


Stress as a Tensor
You might be wondering why the stress at a single point should change from a shear stress to a normal stress or the other way around depending on how we choose to orient our imaginary cut through the bar.
The truth is that it doesn’t. The stress state at a single point within a body will actually have components in the normal and shear directions. The magnitude of the normal and shear components depends on the angle of the plane being used to observe the stresses, as illustrated below.


This is because stress is actually a tensor quantity – at each point within a body the stress state can be represented by three normal stresses and six shear stresses. These stress components are shown on the stress element, a small cube that is used to represent the stress state at a single point within a larger body. You can learn more about the stress tensor and stress element by having a read of our page on stress transformation and Mohr’s circle.

What is Strain?
Strain is a quantity that describes the deformations that occur within a body. Like with stress, we can differentiate between normal strain and shear strain.
Normal Strain
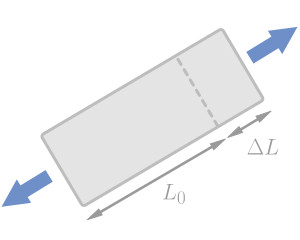
Normal strain is defined as a change in length $\Delta L$ divided by the original length $L_0$. This makes it a dimensionless quantity, that is often expressed as a percentage.

Shear Strain
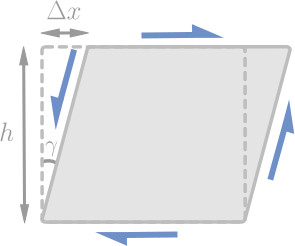
Shear strain is a measure of the deformation caused by a shear stress. It corresponds to the change in angle between two lines that are initially perperpendicular to one another, as shown in the image below. Like normal strain, shear strain is a dimensionless quantity that is usually expressed as a percentage.

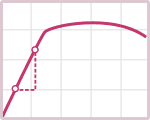
The Stress-Strain Diagram
Stress and strain are two closely linked parameters – it makes sense that the internal forces that develop within a body (stress) depend on how much the body is being deformed (strain).
The relationship between these two parameters can be described using a stress-strain diagram. Stress-strain diagrams are different for different materials. The image below shows typical diagrams for glass, steel and rubber.
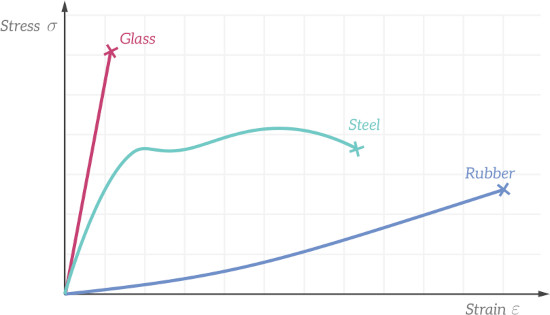

The diagram for a specific material can be obtained by performing a tensile test, which involves applying a known force to a test piece and measuring the normal stress and normal strain in the test piece as the applied force is increased.
For many materials the relationship between stress and strain is linear for relatively low values of stress and strain. In this region the linear relationship between normal stress and normal strain is defined by Hooke’s law, where $E$ is Young’s modulus, a material property that defines the stiffness of a material.
Other important material properties that can be determined from the stress-strain curve include strength, ductility and toughness.
A steel bar is being designed to support a suspended 2000 kg mass, as illustrated below. The bar is 1 m in length and has a circular cross-section. The maximum allowable stress in the bar is 80% of the material yield strength and the selected steel has a yield strength of 300 MPa. What is the minimum allowable radius of the bar, to the nearest 0.1 mm?


0.4 mm
1.1 mm
5.1 mm
6.4 mm
The tensile stress in the bar is:
$$\sigma = \frac{F}{A} = \frac{9.81 \cdot 2000}{\pi r^2}$$
The maximum allowable stress is:
$$\sigma_{max} = 0.8 \sigma_y$$
The limiting radius can be calculated as follows by equating the tensile stress in the bar with the allowable stress:
$$\frac{9.81 \cdot 2000}{\pi r^2} = 0.8\sigma_y$$
$$r = \sqrt{\frac{9.81 \cdot 2000}{\pi 0.8 \sigma_y}} = 5.1 \mathrm{mm}$$
Related Topics
Young's Modulus
Young's modulus is a measure of the stiffness of a material – it describes the relationship between stress and strain.
Strength, Ductility & Toughness
Strength, ductility and toughness are three important material properties that can be determined from a stress-strain curve.